Crossed Bearing
The crossed bearing algorithm can be used when hydrophones are arranged in small clusters, each of which can provide a bearing.
For example a towed hydrophone might contain two groups of hydrophones, with spacing within each group close enough that they can be considered a compact array, which can easily estimate bearings, but spacing between the hydrophone groups large enough that crossing angles can be used to estimate absolute source locations.
If using static equipment, then it may be possible to deploy groups of several multi-channel recorders. Channels within each recorder would be accurately time synchronised, so TDOA measurements from each recorder would provide accurate bearings, however time synchronisation between recorders may not be accurate enough for TDOA measurement, so crossed bearings could be used to combine data from multiple clusters.
The crossed bearing algorithm uses exactly the same internal algorithms as target motion analysis, which crosses bearings from multiple sounds from the same animal from different locations of a single compact array.
Configuration
Select the Crossed Bearings algorithms from the drop down list. Click on the configuration button to the right of the list to select one of three possible crossed bearing algorithms. You may also limit the maximum number of sounds used within the algorithm and select limits (Filters) on reasonable outputs - any localisation result outside these limits will be rejected.
In principle, it is possible to select more than one of the above algorithms, in which case all will be applied and PAMGuard will select the best result based on goodness of fit criteria. Generally, it is recommended that you test the options through simulation and then select one algorithms which is giving the best results. an exception might be when using a moving array, which might sometimes be in a linear line (so 3D location is definitely not possible) and sometimes might (for example as a boat turns) effectively form a plane. In this instance you might run both the 2D and 3D simplex algorithms and the ‘best’ model fit will be selected based on AIC.
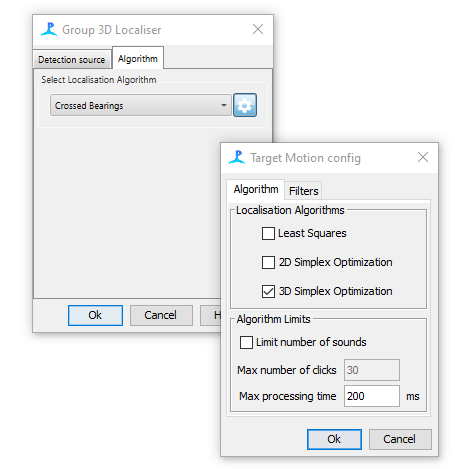
Least Squares
This is the original target motion algorithm developed within PAMGuard. The algorithm is fast, but makes an assumption that all detections are being at points which form a straight line. It is therefore only suitable when there are no more than two hydrophone groups (or when they genuinely are in a straight line).
2D Simplex
This algorithm can deal with any configuration of hydrophones arranges in a planar array and will only estimate positions in two dimensions.
A Simplex algorithm is used to find a point which has the least squares error of bearings from each hydrophone cluster location. This algorithm is slightly more flexible and better at dealing with complex array geometries than the Least Squares algorithm above.
3D Simplex
This algorithm is ideal for volumetric arrays. It can also work with planar arrays, though localisations may be subject to an ambiguity across the plane.
This algorithm is the most flexible and better at dealing with complex array geometries than the Least Squares or 2D Simplex algorithms above, but will fail with unsuitable array geometries.
The algorithm can work with hydrophone clusters of different types, e.g. with one tetrahedral cluster (producing bearings with unambiguous slant and elevation angles) and a pair of hydrophones (producing bearings with an ambiguity about the pair axis). Somewhat surprisingly, you can sometimes get a 3D location from two or more horizontal pairs of hydrophones, so long as they are not all in a line (forming a linear array).