Hyperbolic
The hyperbolic localisation algorithm is a direct implementation of the algorithm described in Gillette and Silverman (2008), although the algorithm was earlier described by Spiesberger and Fristrup (1990). It’s also worth reading Spiesberger (2001) which gives an explanation of the minimum number of hydrophones required for 2D and 3D localisation.
PAMGuard contains both 2D and 3D implementations of the algorithm and will automatically select the appropriate version depending on the shape of the hydrophone array.
A hyperbola is calculated for each pair of hydrophones from the time delay between that hydrophone pair. This requires that accurate time delays can be calculated for the sounds being detected, so accurate time synchronisation for all hydrophones is important. This is generally not a problem for hydrophones cabled to a single acquisition system, but can be highly problematic for
Configuration
To configure, select Hyperbolic from the list of available algorithms. Timing and channel configuration options will be shown.
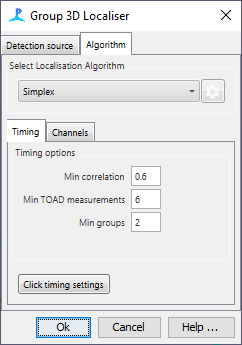
It is possible to set a minimum correlation value for each time delay, any hydrophone pair with a cross correlation value smaller than this being excluded from the minimisation function.
Consequently, it is also possible to set a minimum number of TOAD measurements to use in the localisation, the localisation attempt being aborted if not enough hydrophone pairs can return adequate correlations between signals.
If hydrophones are arranged in groups (e.g. a click detector operating on multiple small hydrophone clusters as in Gillespie et al, (2020) then you can also define a minimum number of groups to use in a localisation.
If the detection source has TDOA timing options available, then these can be accessed through the Timing Settings button.
References
Gillette, M. D., and Silverman, H. F. (2008). “A linear closed-form algorithm for source localization from time-differences of arrival,” IEEE Signal Processing Letters, 15, 1-4.
Spiesberger, J. L., and Fristrup, K. M. (1990). “Passive localization of calling animals and sensing of their acoustic environment using acoustic tomography,” The american naturalist, 135, 107-153
Spiesberger, J. L. (2001). “Hyperbolic location errors due to insufficient numbers of receivers,” The Journal of the Acoustical Society of America, 109, 3076-3079