Localisation Algorithms
PAMGuard allows the user to select a number of localisation algorithms for target motion analysis. The mathematical basis behind these algorithms can be found in the Localisation Techniques section.
The Localisation algorithms utilised in target motion analysis are either 2D or 3D in nature. A 2D algorithm does not consider depth as a variable and will attempt to find the most likely position of the source on the sea surface. A 3D algorithm attempts to localise in all three dimensions.
Referring to the Target Motion Overview section, a single paired hydrophone array will often result in a circular probability distribution of the source location. In 2D this circle become two points and hence the 2D localisation algorithms will often have two results, one for each of the possible points. The straightness of the trackline and uncertainty in hydrophone positions dictates how similar in likelihood each of these results is. Often it will be ambiguous as to which is the more correct location of the animal.
Algorithm Description
Least Squares The least squares algorithm is the least computationally intense of the four. It will only work if the track is relatively straight. The first step of the computation is to fit a straight line to the GPS data and then to project all bearings from that straight line. By using a straight line approximation, it is then possible to use a simple linear regression of the 1/tan(bearing angle) to the animal against their position along the track-line to compute a perpendicular distance and a position along the track-line (Gillespie and Chappell 2002). The regression is carried out for an animal on each side of the trackline and the side with the lowest chi squared taken as the most likely position, where chi squared is the sum of the squares of the difference in measured angles to true angles to the location divided by the expected bearing errors.
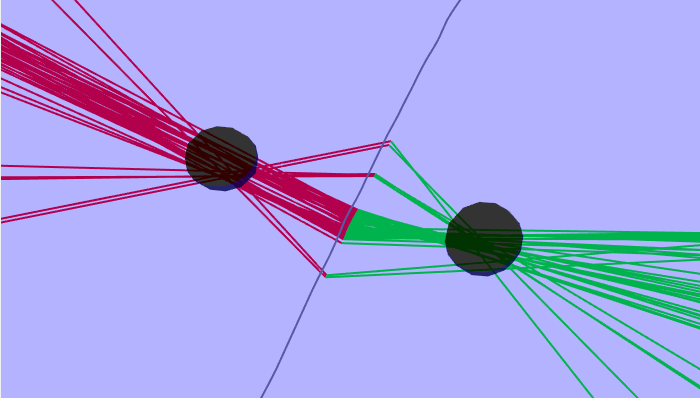 |
|---|
Simplex2D The 2D simplex method, as it’s name implies, uses the Nelder-Mead Simplex optimisation algorithm (available in the apache commons library ) to minimise the chi squared function, where the chi squared is again the sum of the squared differences between the expected and measured angles to any animal location. The difference between the Simplex and the Least Squares method is that the Simplex method can handle large changes in vessel heading. To achieve this however, the algorithm cannot calculate the animal position directly, but must use the Simplex search method which tests many possible positions until it finds the one with the lowest chi squared . While more flexible than the Least Squares method, this inevitably takes considerably longer to execute. The errors calculated by this algorithm are derived from the uncertainty in position of each hydrophone element. These can be set in the hydrophone array manager window .
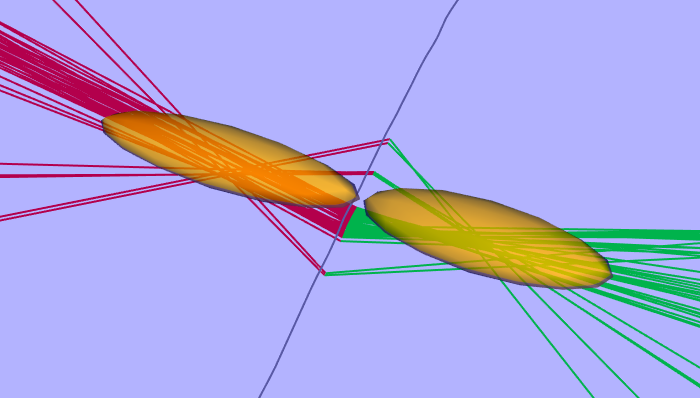 |
|---|
Simplex3D Simplex3D is the 3D version of the Simplex2D algorithm and a very fast 3D localiser. The errors calculated by this algorithm are also derived from the uncertainty in position of each hydrophone element.
 |
|---|
MCMC MCMC is a 3D localisation algorithm based on Markov chain Monte Carlo methods. It is a very computationally intensive algorithm, however, shows the most accurate probability distribution of the source location. The algorithm is extremely sensitive to errors and has several settings which need changed depending on the range distribution of localisations.
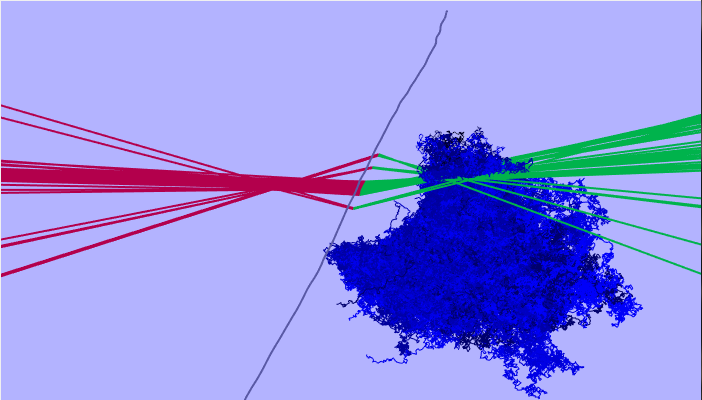 |
|---|
The MCMC localiser uses the errors in hydrophone element positions set in the hydrophone array manager window and the expected error in the time delay measurements to calculate the likely probability distribution of the source location. The error in time delay measurements will generally come from cross correlating two digitised waves and for most species will be around 1 sample. For species, such as harbour porpoises, with narrowband clicks this error should be increased.
The time delay error and other settings for the MCMC localiser can be accessed from the MCMC ‘Settings’ tab in the model control panel.
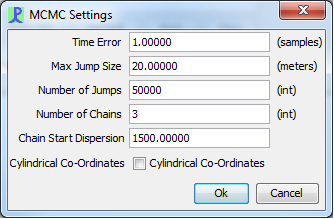 |
|---|
Time Error
Set the error in time delays. Generally this will be 1 sample although for narrowband species this should be set to around 5 samples.
Max Jump Size
The length of each MCMC jump is a random number between 0 and Max Jump Size. If the jump size is set too low it will take the algorithm a long time to find the source location. If the jump size is set too high the probability distribution will not ‘flesh out’ properly. As a rule of thumb the maximum jump size should be 1/100 of the maximum expected detection range.
Number of Jumps
The number of attempted jumps. The more jumps the longer the computation time. If the number of jumps is set too low the algorithm will not ‘flesh out’ the probability distribution of the source location properly and may not reach the source location at all. For 3D localisation without any additional parameters 250000 jumps is usually sufficient.
Number of Chains
The number of Markov Chains used to localise. More chains means more accurate results and will also show whether there is a potential 3D ambiguity in the source location. Each chain runs on separate processor thread.
Chain Start Dispersion
Each Markov chain begins in a random location. The maximum range of these random location is set by Chain Start Dispersion. Generally this should be the maximum detection range of the species in question.
Cylindrical Co-Ordinates
Switching from a Cartesian to a Cylindrical Co-Ordinate system allows MCMC to flesh out circular probability distributions more efficiently.